Final Report
1 Summary
In this project, we implemented three versions of concurrent skip lists: a global locking version, a finegrained
per-pointer locking version, and a Compare-And-Swap(CAS) based lock-free version. The language
and platform we choose are C++ and an 8-core GHC machine respectively. And to support lazy deletion for
our pointer locking version and lock-free version, an open-source C++ garbage collector called Boehm Garbage
Collector is employed. During the evaluation, we constructed several workloads to verify the correctness of our
code and compare the performance of our three implementation versions. We demonstrated that under middle
or low contention workloads, the fine-grained pointer locking version performs better than the global locking
version and that under reads-dominated workloads, compared to pointer locking, the performance can benefit
more from non-blocking lock-free programming, regardless of different contention levels.
The project website: https://lizidong2015.wixsite.com/15618, contains more information
on our project proposal, milestone report, and overall timeline. For source code reference, please navigate to
https://github.com/LongyuYang/Concurrent-Lock-free-Skip-List.
2 Background
Skip list, illustrated by Figure 1, is a very interesting data structure for searching an element in an ordered
sequence. Its probabilistic feature guarantees O(logN) time complexity for search, update, and deletion, yet
its linked-list-like overall structure is much easier to implement compared to tree-like search structures such
as red-black trees. As a result, skip lists are used by many modern applications. For example, the famous
in-memory key-value storage Redis implements its sorted set data structure using a skip list. And the Java
programming language absorbs thread-safe skip lists as a standard library called ConcurrentSkipListMap. In
this project, we will first implement a global locking thread-safe version of our skip list using C++. Next, we
will build a fine-grained per-pointer locking skip list based on algorithms introduced by Pugh [1]. Finally, using
the Compare-and-Swap(CAS) based algorithms proposed by Fraser [2], we will achieve our final lock-free skip
list and compare its performance with our previously implemented locking versions.
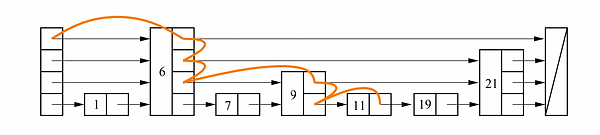
Figure 1: Illustration of searching in a skip list. Source: [2]
3 Approach
3.1 Code Structure
The main source code is located in the /src directory of our project repository, where base.hpp contains
two C++ class template. One is the skip list node template that includes the key-value of a node, the maximal
level of a node, a next array in which next[i] points to the next node at the i-th level, a pointer lock
mutex array to lock corresponding pointers in next array for our per-pointer locking implementations:
template<class _Key, class _Val, bool _init_lock = true>
class skip_list_node {
private:
typedef skip_list_node<_Key, _Val, _init_lock> _node;
std::mutex* pointer_locks;
public:
_Key key;
_Val val;
_Val *v_ptr; // used by lock-free implementation only
_node** next;
size_t level = 0;
bool is_header = false, is_tail = false;
... // member functions are omitted here
};
The other is an abstract class template of our skip list that is inherited by each of our three skip list implementations:
template<class _Key, class _Val, bool _init_lock = true>
class skip_list {
protected:
typedef skip_list_node<_Key, _Val, _init_lock> _node;
_node* header;
_node* tail;
size_t max_level;
... // member functions are omitted here
}
It provides common data structures of skip lists, such as the header node and the tail node, so that each child
class doesn’t need to define them again. It also defines the basic operations of our skip lists using three pure
virtual functions:
virtual _Val get(_Key key) = 0;
virtual void insert(_Key key, _Val val) = 0;
virtual void erase(_Key key) = 0;
In this way, a base pointer of the skip list class can point to different child classes and thus call different
implementations of these operations, which facilitates our testing and evaluation.
3.2 Thread-Unsafe Implementation
To build a correct prototype that our later thread-safe versions can build upon, we first implemented a threadunsafe
version of skip list in src/unsafe.hpp. Inside the unsafe skip list class template, the private
search function starts looking up the target key from the header node at the most top level. Whenever the key
of the current node is equal to or bigger than the target key, the algorithm moves to the next lower level until
the lowest level is reached. The function then returns a left node list where left[i] is the rightmost node
at level i that has the key smaller than the target key, and a right node list where right[i] is the next node
of left[i]. If the key of right[0] equals to the target key, it means that the desired node is found.
The public get operation simply calls this search function and returns the target value if the target key is
found. The public erase operation also calls this search function and removes the node from the list at each
level if the target key is found. And finally, the public insert operation first randomly selects the maximal
level and allocates a new node. It then calls the search function. If the target key already exists, the operation
simply updates the value and returns. Otherwise, it inserts the new node at the desired location of each level
based on the left and right node list returned by the search function.
3.3 Global Locking Version
Based on our correct thread-unsafe implementation, building a global locking thread-safe version can be
straightforward. The code is located in src/glock.hpp and the basic idea is to use a global std::mutex
per instance to obtain a lock upon entering each public operation and release the lock when the operation returns:
virtual _Val get(_Key key) {
/* LOCK */
const std::lock_guard<std::mutex> lock(global_lock);
...
};
3.4 Fine-grained Per-Pointer Locking Version
We implement our fine-grained per-pointer locking skip list based on algorithms proposed by Pugh [1].
The corresponding source code file is src/pointer lock.hpp and the class template that inherits the base
skip list is pointer lock skip list. Each skip list node class template has a lock array called
pointer locks in which pointer locks[i] (0 <= i < level) is a lock for pointer next[i]
and pointer locks[level] is a lock for protecting change of level during insertion and deletion.
3.4.1 Helper Functions
The private search member function does the same thing as the search function in our thread-unsafe
implementation. The private get lock(x, key, i) function locks the next pointer at a certain level immediately
in front of the target key. It takes three input parameters, the current observed before-target node x,
the target key key, and the level i. Inside this function, it tries to advance x at the i-th level since some other
threads might successfully insert some nodes in the middle of x and the target node after x is observed. After
it can’t advance anymore, it tries to lock x->next[i] and double-checks whether x->next[i] is equal or
bigger than the target key. If the check fails, it unlocks x->next[i] and continues to advance x and tries
to lock x->next[i] again. Upon successfully obtaining the lock, the get lock function finally returns the
node x with its x->next[i] locked.
3.4.2 Get and Insert Operations
The public get operation simply calls the search function without obtaining any lock. The insert
operation, however, is more complex. The basic idea is to lock the pointer immediately in front of the desired
location and insert the new node level by level.
The insert operation first calls the search function to obtain a left node list where left[i] is the
rightmost node at level i that has the key smaller than the target key. Then it calls x = get lock(x, key,
0) to lock the lowest next pointer immediately in front of the target key. If the key of x->next[0] equals to
the target key, it means that the key already exists and the algorithm changes the value of x->next[0], unlocks
x->next[0], and returns instantly. Otherwise, a new node named new node is allocated and randomly
selects a new level named new level. The algorithm then locks new level to protect the level from being
updated by other threads. Then it began to insert the new node from level 0 to level new level-1. For
insertion at each level i, the algorithm calls x = get lock(left[i], key, i) to lock the next pointer
that needs to be updated (except for level 0 because the lock has already been obtained), inserts new node in
the middle of x and x->next[i] and unlocks x->next[i]. After the insertion completes, the algorithm
finally releases the lock on new level and returns.
3.4.3 Erase Operation
The public erase operation is more complicated. The basic idea is to remove the target node from its most
top level to level 0, which is a somewhat reverse process of new node insertion.
Similar to the insert operation, the algorithm first also calls the search function to obtain the left
node list. For removal at each level i, suppose the target node is y, the algorithm also calls x = get lock(left[i],
key, i) to lock x->next[i] where x is immediately before y at level i. Then it also locks y->next[i]
and remove y from the middle of x and y->next[i]. However, one problem arises here: what if there are
other threads currently working on the deleted node y? To tackle this issue, the algorithm uses a lazy deletion
scheme: it removes y from level i but makes y->next[i] point to x. In this way, the deletion will not affect
threads that are currently working on node y, ensuring that those threads can still make progress.
The lazy deletion scheme, however, imposes another challenge: it’s not easy to know whether there are
threads working on a deleted node or not, in other words, whether the memory of a deleted node can be safely
released. If we use programming languages such as Java, this issue can be taken care of by the runtime system
because it periodically garbage-collects unused memory. However, the reality is that we are using C++ which
traditionally has no GC features. To prevent our program from memory leakage, fortunately, we found an
open-source C++ garbage collector called Boehm Garbage Collector. In the constructor of our skip list, we
first allocate the header node using GC MALLOC UNCOLLECTABLE primitive, indicating that the header is not
garbage-collectible but can be treated as the root of other memory allocations. This means that the garbage
collector will scan the header and track other memory locations referenced by pointers inside of the header.
Then in the insert function, we allocate a new node by using GC MALLOC primitive, which indicates that
the node is garbage-collectible as long as no other pointer is referencing to it. By doing garbage collections,
we ensure the correctness of our fine-grained locking version during erase operations while preventing the
program from memory leakage. The garbage collector is also very useful for our lock-free version that employs
a pointer-marking-based lazy deletion scheme, which will be discussed in the next section.
3.5 Lock-Free Version
By referring to CAS-based algorithms introduced by [2], we achieved our final non-blocking lock-free skip
list in src/lock free.hpp.
3.5.1 Pointer Marking
One problem for lock-free implementation is the ’disappearing node’ problem, where a new node is inserted
after a current node but another thread removes the current node concurrently, leaving the new node never
visible. To solve this problem, a pointer marking scheme is used to mark the next pointer of the deleted node
before actually removing it from the list. Since the lowest bit of a pointer is always zero, this marking scheme
can be implemented by manipulating the lowest bit of each pointer. In our lock-free implementation, three
helper functions are used for pointer marking:
_node* mark(_node* p) { return (_node*)(uintptr_t(p) | 1);}
_node* unmark(_node* p) { return (_node*)(uintptr_t(p) & (˜1));}
bool is_marked(_node* p) { return uintptr_t(p) & 1;}
And another helper function is used to mark all next pointers of a node:
void mark_node_ptrs(_node* x) {
for (ssize_t i = x->level - 1; i >= 0; i--) {
_node* x_next;
do {
x_next = x->next[I];
if (is_marked(x_next)) break;
} while (CAS(&x->next[i], x_next, mark(x_next)) != x_next);
}
}
For each level of the node, the above function spins on a CAS operation to mark the next pointer of that level.
Upon the CAS succeeds, the function moves to the next level until the lowest level is reached.
3.5.2 Search Helper Function
Similar to search function of our other implementations, the private search function of our lock-free
version looks up the target key and returns a left node list and a right node list where left[i] is the
rightmost node that has smaller-than-target key and right[i] == left[i]->next[i] for level i. It’s
also more complicated since it has the responsibility of identifying marked nodes and removing them from the
list. During search at each level i, the algorithm will skip a sequence of marked nodes until it finds a valid
unmarked pair where the key of the first node is less than the target key and that of the second node is equal-orgreater
to the target key. It then removes the sequence of marked nodes in the middle of this unmarked pair by
directing connecting the unmarked pair using CAS. Upon this point, the sequence of marked nodes is deleted
from the list and can be further garbage-collected by Boehm Garbage Collector.
3.5.3 Get and Erase Operations
The get operation simply calls the search function and returns the value if the node is found. The erase
operation also calls the search function. And if the target key is found, the right[0] will be the node to be
deleted. To logically remove this node, the algorithm first sets the value of right[0] to NULL by spinning
on a CAS operation. After the CAS succeeds, it will call mark node ptrs function to mark all next pointers
of right[0] so that no new node will be connected right after right[0]. Finally, the deleted node is
guaranteed to be removed from the list by another call to the search function.
3.5.4 Insert Operation
The public insert function first calls the search function to look up the desired key. If the target node
is found, i.e. right[0]->key == key, the algorithm tries to update the value of right[0] by spinning
on a CAS operation. During the spinning, if it observes that the current value of right[0] is already NULL, it
means that the node has been logically deleted from the list by an erase operation. In this case, the algorithm
calls mark node ptrs function to mark all next pointers of right[0], makes another call to the search
function to ensure the node is removed from the list, and goes to the beginning of insert function to retry the
execution. Otherwise, the CAS succeeds, the value of right[0] is updated, and the function returns instantly.
On the other hand, if the desired key doesn’t exist in the list, the algorithm will allocate a new node
new node and randomly select a new level new level. Then it will connect each level of new node with
nodes in the right list. After that, a CAS operation tries to connect left[0] with new node[0], which
will make the new node globally visible. If this CAS fails, it will go to the beginning of the insert function to
retry the execution. Otherwise, the algorithm began to connect left[i] with new node[i] for each level i
> 0 by spinning on a CAS operation. If the CAS fails, it means that the left[i] and right[i] are outdated
and the algorithm will retry executing search function to get the new left and right list. There are other
circumstances inside the nested spinning loop that need to be taken care of. One particular circumstance is that
if the next pointer of new node is marked, it means that another thread has deleted the node being inserted. In
this case, the algorithm will break the spinning loop and give up insertion.
4 Evaluation
To evaluate the correctness of the performance of our code, we used one GHC machine that has an 8-core 3.0
GHz Intel Core i7 processor. Each test program is located in the tests/ directory and can be directly compiled
and executed by initiating corresponding commands in the Makefile. Since the Boehm Garbage Collector
doesn’t support high-level thread libraries such as OpenMP very well, we directly used Linux pthreads
library to spawn and synchronize threads.
4.1 Correctness
4.1.1 Thread-Unsafe Version
The tests/test unsafe.cpp initializes a unsafe skip list<int, int> instance and another
std::map for correctness check. The program performs 220 operations consisting of 75% get, 12.5%
insert, and 12.5% erase. The skip list and reference std::map are initialized with integers ranging
from 0 to 215. For each operation, it randomly selects a key from the similar data range to perform the corresponding
operation. During get operation, the test program will check the correctness by comparing the result
from our skip list and that from the reference std::map. If the results are mismatched, the program will print
the error message and exit right away.
To run this test, simply initiate the command make test unsafe.
4.1.2 Thread-Safe Version
It’s difficult to verify the correctness of our three thread-safe versions. Even though the algorithm is proved
to be correct (For instance, the correctness of the per-pointer lock algorithm is proved in [1]), there is still a
chance of introducing subtle bugs in terms of implementation. To tackle this issue, a workload consisting of very
high contention has been built to empirically evaluate the correctness of our three thread-safe implementations.
On the 8-core GHC machine, we first spawned 8 threads to concurrently insert 215 consecutive integers to the
skip list. Then a large outer loop will iterate on the range of 1 to 215. For each iteration step, an intense inner
loop is executed by the 8 threads, each of which performs high-contention operations on its assigned position by
continuously get, erase, and insert to the position a fixed number of times. After this, we will examine
the value of each of the 215 integers and finally, erase all numbers in the skip list concurrently. Using this
empirical workload, we found that even the most subtle bug and deadlock can be exposed within less than two
runs of the test.
The source code of this empirical test is located inside tests/test thread safe.cpp. To run this
test, simply initiate the command make test glock, make test pointer lock, or test lock free
to check the correctness of our global locking version, pointer locking version, and lock-free version, respectively.
4.2 Performance
To compare the performance of our three thread-safe implementations, we construct a benchmark workload
inspired by [2]. At the beginning of the evaluation, the skip list is initialized by inserting K integers ranging
from 0 to K − 1. Then N number of threads are spawned, each of which performs a sequence of randomly
chosen operations on a randomly selected integer from the same range for 10 seconds. After all threads complete
execution, each thread returns the number of operations performed. Then thread 0 sums up the total number
of operations and calculated the final performance result measured by the mean CPU time (micro-seconds)
per operation. Following [2], the distribution of the three operations is 12.5% insert, 12.5% erase, and
75% get, which simulates a reads-dominated workload that are common in real-world parallel programs. To
conduct the performance evaluation more thoroughly, a different write-dominated workload inspired by [3] is
also reported, which will be discussed in Section 4.2.3.
4.2.1 Effect of Contention
We evaluate the effect of different contention levels by varying the data range K from 24 to 219 and fixing
the number of threads. Obviously, when K is relatively small and is on the same magnitude with the thread
count, the contention on the skip list is high. By contrast, when K significantly exceeds the thread count, the
probability of operating on the same node is smaller and thus the contention level is relatively low. Figure 2 and
3 show the effect of contention on the performance of our three implementations by fixing the thread count to
16 and 32 respectively:

Figure 2: Effect of contention level on the performance when the thread count is 16.
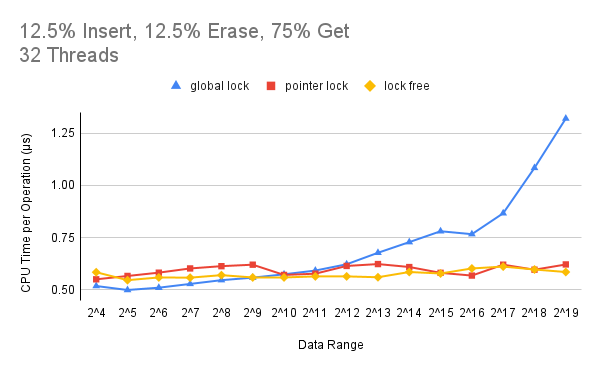
Figure 3: Effect of contention level on the performance when the thread count is 32.
From these two figures, we can see that when the contention is high (K < 29), the global locking version has
a performance advantage over both of our pointer locking version and lock-free version. The reason is that under
very high contention, the overhead associated with obtaining and releasing a large number of fine-grained locks
dominates the execution for pointer locking version, and that the overhead associated with spinning on CAS
operations and retrying the search function dominates the execution for the lock-free version. However, in
this high contention zone, the lock-free version is still better than the pointer locking version since the lock-free
implementation is guaranteed to make system-wide progress while the pointer locking implementation might
block the progress for a long time if a thread holding the lock is very slow or context switched off the core by
the operating system.
Figure 2 and 3 also indicate that when the data range becomes larger(K > 212), the performance of the
global locking version degrades significantly since it’s unnecessary to lock the whole data structure when some
non-adjacent nodes could have been operated in parallel. In this data range area, the contention level on a node
is of middle to low level and the complexity of pointer locking and lock-free implementations begins to pay off.
To run the above test program for evaluating the effect of contention, simply run make test performance 3
and the default thread count will be 16. To change the thread count for this test, open the performance 3.sh
at the tests/scripts/ directory and change the value of -t option at line 14.
4.2.2 Scalability
Now we fix the data range and increase the number of threads from 1 to 100 to evaluate the scalability of
our three implementations. Figure 4 shows the performance results when the data range K is set to 27. Under
this data range, the contention level is very high and all of our three implementations don’t scale as the thread
count increases. In fact, the performance degrades linearly until the thread count is larger than the core count.
The reason behind this is that under such high contention, the synchronization overhead accounts for a large
proportion of the total execution time and thus the performance doesn’t benefit from the parallel execution when
adding more threads. On the other hand, even though the global locking version is the best in performance most
of the time, the lock-free version still has an advantage over the pointer-locking version especially when the
thread count is higher than the core count.
Figure 5 shows the results when the data range K is set to 219, which means that the contention level is
very low. From this figure, we can see that under a large data range, the global locking version has the worst
CPU time per operation since it’s not necessary to lock the whole data structure and block concurrent search
and modification on non-adjacent nodes. Also, the pointer locking version and the lock-free version experience
a great performance improvement when the thread count rises from 1 to 4. But then the performance begins to
degrade as the thread count goes from 4 to 8. And finally, the CPU time per operation stabilizes at around 0.6,
which is still better than that of a sequential program. This indicates that although the program doesn’t scale
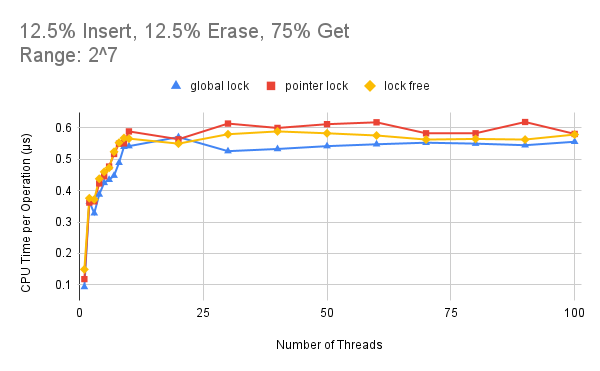
Figure 4: Effect of number of threads on the performance when the data range is set to 2^7
well especially when the thread count exceeds the core count, parallel executions can still be beneficial. On
the other hand, the lock-free version performs slightly better than the pointer locking version especially when
the thread count greatly exceeds the core count. But the benefit of lock-free is not as significant as that when
the contention is intense. One reason is that lock collision is infrequent under low contention level so that the
pointer locking version can perform as well as the non-blocking lock-free version. Another possible explanation
is that when the data range is wide, one retry for the search function inside the lock-free version is extremely
expensive compared to simply waiting for a lock inside the pointer locking version.
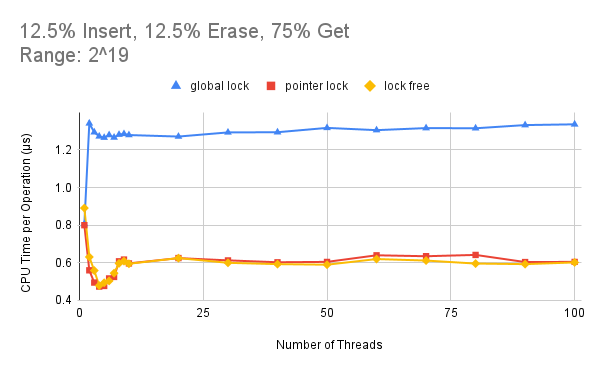
Figure 5: Effect of number of threads on the performance when the data range is set to 2^19
To run the above test program for evaluating the effect of the thread count, simply run make test performance 2
and the default data range is set to 19. To change the data range, open the performance 2.sh at the
tests/scripts/ directory and change the value of -r option at line 14.
4.2.3 Effect of Operation Distribution
We also reported the result using a different operation distribution inspired by [3]. We change the distribution
of the three operations to 50% insert, 50% erase, and 0% get, which simulates a writes-dominated
workload rather than a reads-dominated one discussed in previous sections. Figure 6 illustrates the performance
of our three implementations by varying the data range and fixing the number of threads to 16, which
is similar to the experiment set in Figure 2 except for the different operation distribution. From Figure 6, it
can be concluded that under a writes-dominated workload, the pointer locking version is almost always the
best in performance. While the global locking version experiences a performance degradation as the data range
goes up, the performance of the lock-free locking version stays stable and is slightly worse than that of the
pointer locking version. A possible explanation is that the overhead of spinning on CAS operations and retrying
the search function counteracts the benefit of non-blocking and progress guarantee. Particularly, inside the
insert operation, inserting a new node to every level of its adjacent nodes has the chance of observing stale
adjacent pointers, causing a costly retrying call to the search function. When the data range is small, the
probability of collision is high so that the retry is frequent. On the other hand, when the data range is large,
even though the probability of collision is relatively smaller, one retry of the search function is extremely
expensive because it has to begin from the start and traverse over a large number of nodes before getting to the
desired location again.
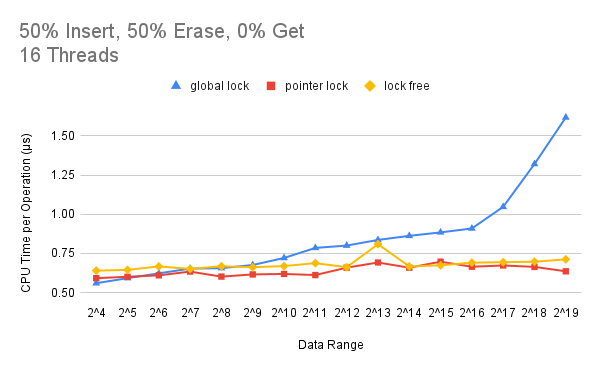
Figure 6: Effect of contention level using a writes-dominated workload when the thread count is 16.
5 Credit
.jpg)
Based on task assignments in Table 1, the total credit should divide to 50%-50%.
References
[1] W. Pugh, “Concurrent maintenance of skip lists,” Department of Computer Science, University of Maryland,
06 1990.
[2] K. Fraser, “Practical lock-freedom,” PhD thesis, University of Cambridge, 01 2004.
[3] M. Herlihy, Y. Lev, V. Luchangco, and N. Shavit, “A provably correct scalable concurrent skip list,” in
Conference On Principles of Distributed Systems (OPODIS). Citeseer, p. 103, Citeseer, 2006.